Πριν από 243 χρόνια ο διάσημος μαθηματικός Leonhard Euler έθεσε ένα ερώτημα. Aν έξι συντάγματα στρατού έχουν έξι αξιωματικούς, έξι διαφορετικών βαθμών, μπορούν να είναι διατεταγμένα σε τετράγωνο σχηματισμό έτσι ώστε καμία σειρά ή στήλη να μην επαναλαμβάνει ούτε έναν βαθμό και ούτε ένα σύνταγμα;
Αφού έψαξε μάταια για μια λύση, ο Euler δήλωσε ότι το πρόβλημα ήταν αδύνατο και πάνω από έναν αιώνα αργότερα, ο Γάλλος μαθηματικός Gaston Tarry απέδειξε ότι είχε δίκιο.
60 χρόνια αργότερα, όταν η έλευση των υπολογιστών αφαίρεσε την ανάγκη για επίπονη δοκιμή κάθε πιθανού συνδυασμού με το χέρι, οι μαθηματικοί Parker, Bose και Shrikhande απέδειξαν ένα ακόμη ισχυρότερο αποτέλεσμα. Όχι μόνο είναι αδύνατο το τετράγωνο έξι επί έξι να λυθεί, αλλά είναι το μόνο μέγεθος τετραγώνου εκτός από το δύο προς δύο που δεν έχει καθόλου λύση.
Τώρα, στα μαθηματικά, μόλις αποδειχθεί ένα θεώρημα, αποδεικνύεται για πάντα. Μπορεί λοιπόν να εκπλήσσει το γεγονός ότι μια εργασία του 2022, που δημοσιεύτηκε στο περιοδικό Physical Review Letters, έχει βρει μια λύση. Υπάρχει όμως ένα κόλπο σε όλο αυτό.
Οι αξιωματικοί πρέπει να υπάρχουν σε μια κατάσταση κβαντικής διεμπλοκής.
«Νομίζω ότι η έρευνα τους είναι πολύ εντυπωσιακή», είπε στο Quanta Magazine εκείνη την εποχή η κβαντική φυσικός Gemma De las Cuevas, η οποία δεν συμμετείχε στην εργασία. «Υπάρχει πολλή κβαντική μαγεία εκεί μέσα. Και όχι μόνο αυτό, αλλά μπορείς να νιώσεις σε όλη την εργασία την αγάπη των ερευνητών για το πρόβλημα».
Ο γρίφος του Euler και η λύση των κβαντικών επιστημόνων
Για να εξηγήσουμε τι συμβαίνει, ας ξεκινήσουμε με ένα κλασικό παράδειγμα. Το πρόβλημα «36 Αξιωματικών» του Euler, όπως είναι γνωστό, είναι ένας ειδικός τύπος μαγικού τετραγώνου που ονομάζεται «ορθογώνιο λατινικό τετράγωνο» ακριβώς όπως δύο sudoku που πρέπει να λύσετε ταυτόχρονα στο ίδιο πλέγμα. Για παράδειγμα, ένα ορθογώνιο λατινικό τετράγωνο τέσσερα επί τέσσερα μπορεί να μοιάζει με αυτό:
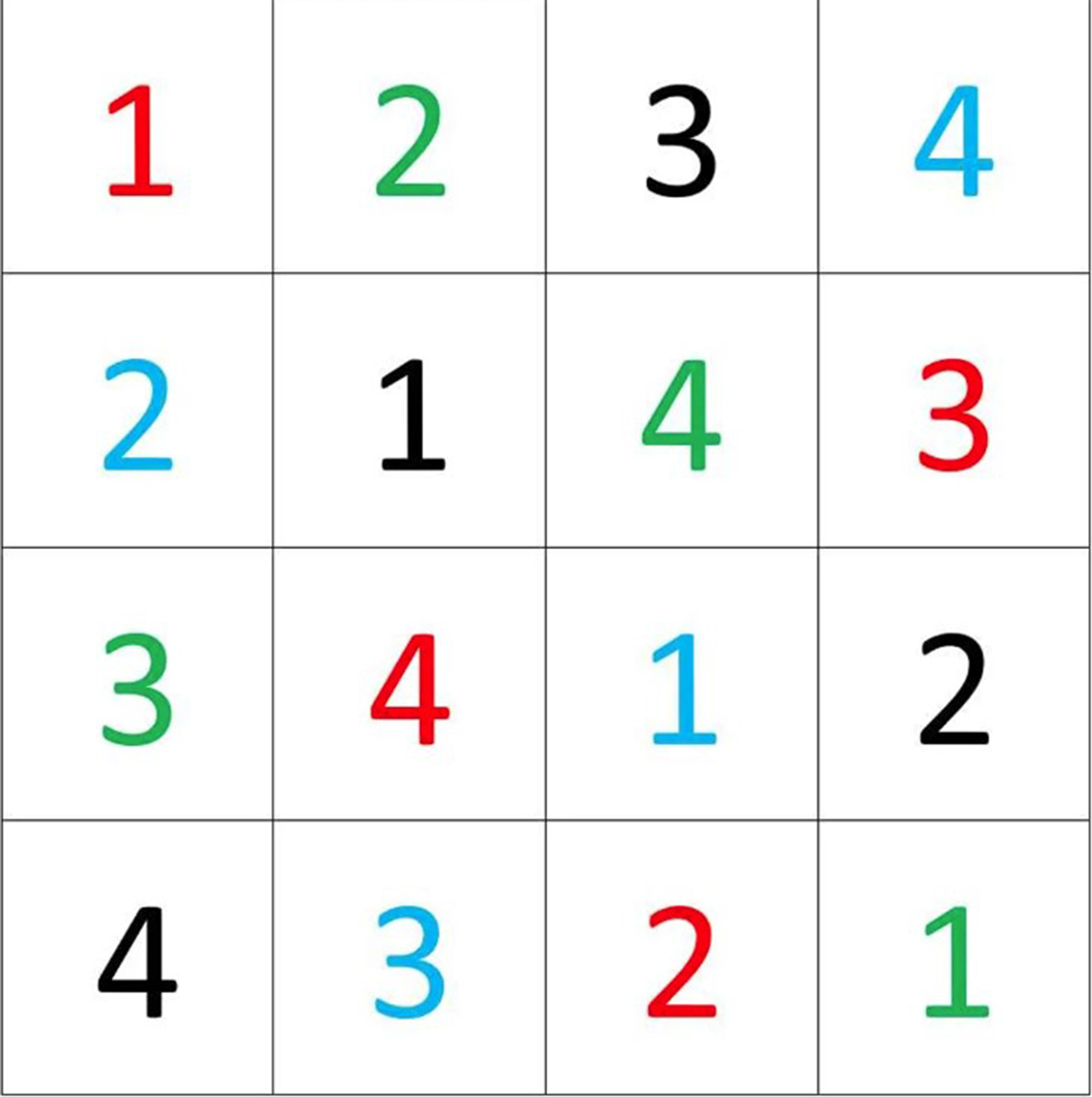
Κάθε τετράγωνο στο πλέγμα ορίζεται με σταθερό αριθμό και σταθερό χρώμα. Το αρχικό πρόβλημα έξι προς έξι του Euler είναι αδύνατο. Ωστόσο, στον κβαντικό κόσμο, τα πράγματα είναι πιο ευέλικτα. Τα πράγματα υπάρχουν σε υπερθέσεις καταστάσεων (State of Superpotition).
Με βασικούς όρους, αυτό σημαίνει ότι κάθε δεδομένος στρατηγός μπορεί να είναι πολλαπλές τάξεις πολλαπλών συνταγμάτων ταυτόχρονα. Χρησιμοποιώντας το πολύχρωμο παράδειγμά με διπλό sudoku, θα μπορούσαμε να φανταστούμε ένα τετράγωνο στο πλέγμα να είναι γεμάτο, ας πούμε, με μια υπέρθεση ενός πράσινου 2 και ενός κόκκινου 1.

Με την πρώτη ματιά, μπορεί να φαίνεται ότι η ομάδα έκανε την δουλειά της πολύ πιο δύσκολη. Όχι μόνο έπρεπε να λύσει ένα διπλό sudoku έξι επί έξι που ήταν γνωστό ότι ήταν αδύνατο στο κλασικό περιβάλλον, αλλά τώρα έπρεπε να το κάνει σε πολλαπλές διαστάσεις ταυτόχρονα.
Ευτυχώς, όμως, οι επιστήμονες είχαν μερικά πράγματα με το μέρος τους. Πρώτον, μια κλασική σχεδόν λύση που θα μπορούσαν να χρησιμοποιήσουν αρχικά και δεύτερον, τη φαινομενικά μυστηριώδη ιδιότητα της κβαντικής διεμπλοκής.
Παραδείγματα για την κατανόηση της κβαντικής διεμπλοκής και την λύση του γρίφου
Με απλά λόγια, δύο καταστάσεις στη κβαντική φυσική λέγεται όταν μια θέση μπλέκεται με μια άλλη.
Ως κλασική αναλογία, ας φανταστούμε ότι ένας φίλος μας έχει δύο παιδιά, το Α και το Β του ίδιου φύλου. Αυτό σημαίνει ότι το να γνωρίζουμε ότι το παιδί Α είναι κορίτσι μας λέει με βεβαιότητα ότι το παιδί Β είναι επίσης κορίτσι και τα δύο φύλα των παιδιών είναι μπλεγμένα.
Η μια κατάσταση σας λέει απολύτως τα πάντα για την άλλη και όταν συμβαίνει, ονομάζεται «κατάσταση απολύτως μπερδεμένη»(AME). Ένα άλλο παράδειγμα μπορεί να είναι η ανατροπή νομισμάτων. Για παράδειγμα, αν η Αλίκη και ο Μπομπ γυρίσουν ο καθένας ένα νόμισμα και η Αλίκη τύχει κορώνα, τότε αν τα νομίσματα είναι μπερδεμένα με όρους κβαντικής φυσικής, ο Μπομπ ξέρει χωρίς να κοιτάξει ότι έχει γράμματα και το αντίστροφο.
Είναι αξιοσημείωτο ότι η λύση σε αυτό το πρόβλημα του κβαντικού γρίφου αποδείχθηκε ότι είχε αυτή την ιδιότητα και αυτό αποκτά πραγματικά ενδιαφέρον. Το παραπάνω παράδειγμα λειτουργεί για δύο νομίσματα και για τρία, αλλά για τέσσερα, είναι αδύνατο.
Όπως συνειδητοποίησαν οι συγγραφείς, το «πρόβλημα των 36 Αξιωματικών» δεν είναι σαν το ρίξιμο των ζαριών. Είναι περισσότερο σαν να ρίχνουμε ζάρια που είναι μπερδεμένα μπερδεμένα με όρους κβαντικής φυσικής.
«Η Αλίκη επιλέγει οποιαδήποτε δύο ζάρια και τα ρίχνει, λαμβάνοντας ένα από τα 36 εξίσου πιθανά αποτελέσματα, καθώς ο Μπομπ ρίχνει τα υπόλοιπα. Εάν ολόκληρη η κατάσταση είναι AME, η Αλίκη μπορεί πάντα να συμπεράνει το αποτέλεσμα που προκύπτει στο μέρος του Bob», εξηγούν.
«Επιπλέον, μια τέτοια κατάσταση επιτρέπει σε κάποιον να τηλεμεταφέρει οποιαδήποτε άγνωστη κβαντική κατάσταση δύο ζαριών, από οποιουσδήποτε δύο ιδιοκτήτες δύο υποσυστημάτων στο εργαστήριο που έχει τα δύο άλλα ζάρια της μπερδεμένης κατάστασης του τετραμερούς συστήματος», συνεχίζουν οι συγγραφείς. «Αυτό δεν είναι δυνατό εάν τα ζάρια αντικατασταθούν από νομίσματα δύο όψεων.»
Επειδή αυτά τα συστήματα AME μπορούν συχνά να εξηγηθούν χρησιμοποιώντας ορθογώνια λατινικά τετράγωνα, οι ερευνητές γνώριζαν ήδη ότι υπάρχουν για τέσσερα άτομα που ρίχνουν ζάρια με οποιονδήποτε αριθμό πλευρών. Οποιαδήποτε, δηλαδή, εκτός από δύο ή έξι. Αυτά τα ορθογώνια λατινικά τετράγωνα δεν υπάρχουν, επομένως δεν μπορούν να χρησιμοποιηθούν για να αποδειχθεί η ύπαρξη μιας κατάστασης AME σε αυτή τη διάσταση.
Ωστόσο, βρίσκοντας μια λύση στο πρόβλημα του Euler, οι ερευνητές είχαν κάνει κάτι εκπληκτικό. Βρήκαν ένα σύστημα AME τεσσάρων μερών της διάστασης έξι. Κάνοντας αυτό, μπορεί ακόμη και να έχουν ανακαλύψει ένα εντελώς νέο είδος AME, ένα χωρίς ανάλογο σε ένα κλασικό σύστημα.
Συμπεράσματα επιστημόνων μετά τη λύση του γρίφου
«Ο Euler ισχυρίστηκε το 1779 ότι δεν υπάρχει λύση. Η απόδειξη, από τον Tarry, ήρθε μόνο 121 χρόνια αργότερα το 1900», γράφουν οι επιστήμονες. «Έπειτα από άλλα 121 χρόνια, έχουμε παρουσιάσει μια λύση στην κβαντική έκδοση του προβλήματος, όπου οι αξιωματικοί μπορούν να μπερδευτούν».
«Ο κβαντικός σχεδιασμός που παρουσιάζεται εδώ πιθανότατα θα πυροδοτήσει περαιτέρω έρευνα στο εκκολαπτόμενο πεδίο της κβαντικής διεμπλοκής», καταλήγουν.

